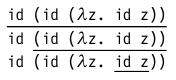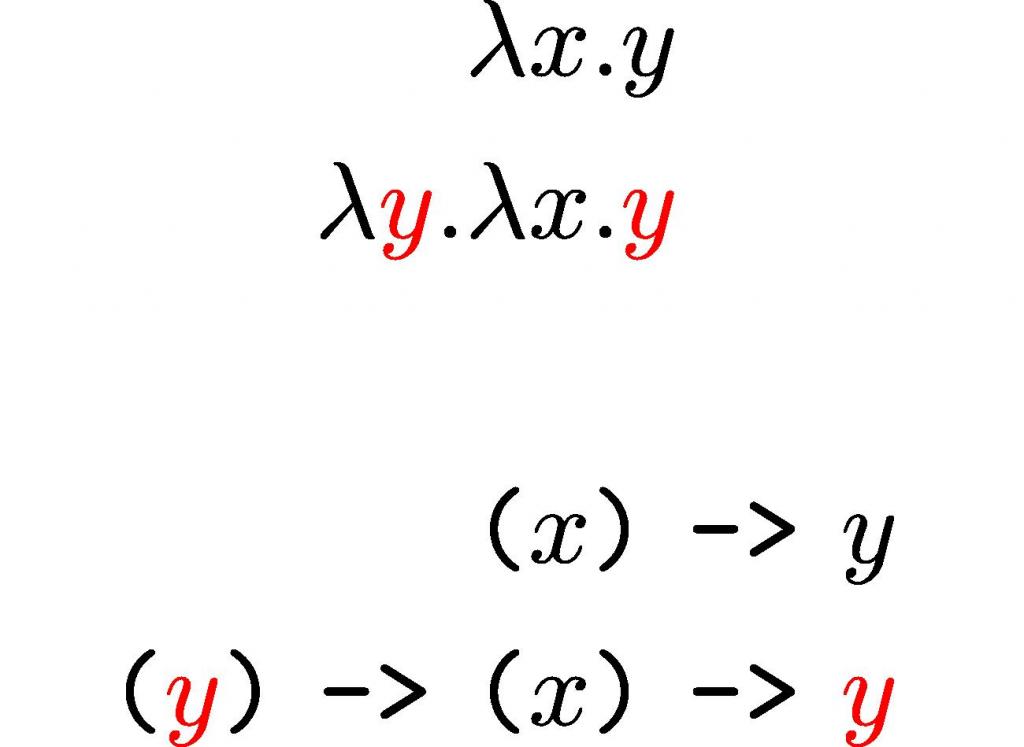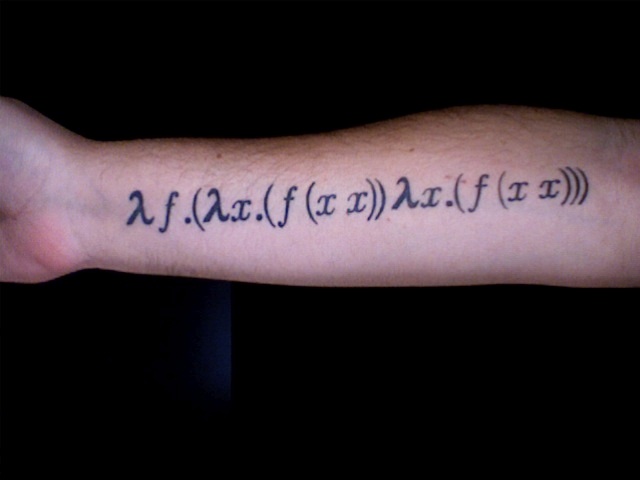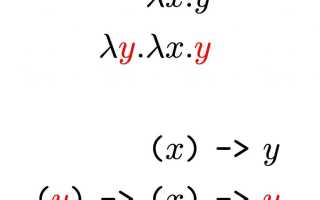Что означает лямбда в отношении лямбда ст c v

Что обозначает лямбда в отношении лямбда ct c v

Начнём мы с традиционного (но краткого) экскурса в историю. В 30-х годах прошлого века перед математиками встала так называемая проблема разрешения (Entscheidungsproblem), сформулированная Давидом Гильбертом. Суть её в том, что вот есть у нас некий формальный язык, на котором можно написать какое-либо утверждение. Существует ли алгоритм, за конечное число шагов определяющий его истинность или ложность? Ответ был найден двумя великими учёными того времени Алонзо Чёрчем и Аланом Тьюрингом. Они показали (первый — с помощью изобретённого им λ-исчисления, а второй — теории машины Тьюринга), что для арифметики такого алгоритма не существует в принципе, т.е. Entscheidungsproblem в общем случае неразрешима.

Так лямбда-исчисление впервые громко заявило о себе, но ещё пару десятков лет продолжало быть достоянием математической логики. Пока в середине 60-х Питер Ландин не отметил, что сложный язык программирования проще изучать, сформулировав его ядро в виде небольшого базового исчисления, выражающего самые существенные механизмы языка и дополненного набором удобных производных форм, поведение которых можно выразить путем перевода на язык базового исчисления. В качестве такой основы Ландин использовал лямбда-исчисление Чёрча. И всё заверте…

λ-исчисление: основные понятия

Синтаксис

В основе лямбда-исчисления лежит понятие, известное ныне каждому программисту, — анонимная функция. В нём нет встроенных констант, элементарных операторов, чисел, арифметических операций, условных выражений, циклов и т. п. — только функции, только хардкор. Потому что лямбда-исчисление — это не язык программирования, а формальный аппарат, способный определить в своих терминах любую языковую конструкцию или алгоритм. В этом смысле оно созвучно машине Тьюринга, только соответствует функциональной парадигме, а не императивной.

Мы с вами рассмотрим его наиболее простую форму: чистое нетипизированное лямбда-исчисление, и вот что конкретно будет в нашем распоряжении.

Термы:

переменная:	x
лямбда-абстракция (анонимная функция):	λx.t , где x — аргумент функции, t — её тело.
применение функции (аппликация):	f x , где f — функция, x — подставляемое в неё значение аргумента

Применение функции левоассоциативно. Т.е. s t u — это тоже самое, что (s t) u
Аппликация (применение или вызов функции по отношению к заданному значению) забирает себе всё, до чего дотянется. Т.е. λx. λy. x y x означает то же самое, что λx. (λy. ((x y) x))
Скобки явно указывают группировку действий.

Процесс вычисления

Рассмотрим следующий терм-применение:

Существует несколько стратегий выбора редекса для очередного шага вычисления. Рассматривать их мы будем на примере следующего терма:

который для простоты можно переписать как

(напомним, что id — это функция тождества вида λx.x )

Читайте также:

Как подключить стационарный телефон к компьютеру для звонков

В этом терме содержится три редекса:

Недостатком стратегии вызова по значению является то, что она может зациклиться и не найти существующее нормальное значение терма. Рассмотрим для примера выражение

(λx.λy. x) z ((λx.x x)(λx.x x))

Ещё одна тонкость связана с именованием переменных. Например, терм (λx.λy.x)y после подстановки вычислится в λy.y . Т.е. из-за совпадения имён переменных мы получим функцию тождества там, где её изначально не предполагалось. Действительно, назови мы локальную переменную не y , а z — первоначальный терм имел бы вид (λx.λz.x)y и после редукции выглядел бы как λz.y . Для исключения неоднозначностей такого рода надо чётко отслеживать, чтобы все свободные переменные из начального терма после подстановки оставались свободными. С этой целью используют α-конверсию — переименование переменной в абстракции с целью исключения конфликтов имён.

Так же бывает, что у нас есть абстракция λx.t x , причём x свободных вхождений в тело t не имеет. В этом случае данное выражение будет эквивалентно просто t . Такое преобразование называется η-конверсией.

На этом закончим вводную в лямбда-исчисление. В следующей статье мы займёмся тем, ради чего всё и затевалось: программированием на λ-исчислении.

Лямбда-выражения являются одним из наиболее мощных дополнений в C++11 и продолжают развиваться с каждым новым стандартом языка. В этой статье мы пройдемся по их истории и посмотрим на эволюцию этой важной части современного C++.

Я решил взять код у Томаса (с его разрешения!), описать его и создать отдельную статью.

Мы начнем с изучения C++03 и с необходимости в компактных локальных функциональных выражениях. Затем мы перейдем к C++11 и C++14. Во второй части серии мы увидим изменения в C++17 и даже взглянем на то, что произойдет в C++ 20.

Читайте также:

Где могут двигаться пешеходы в жилой зоне

С самого начала STL std::algorithms , такие как std::sort , могли принимать любой вызываемый объект и вызывать его для элементов контейнера. Однако в C++03 это предполагало только указатели на функции и функторы.

Но проблема заключалась в том, что вы должны были написать отдельную функцию или функтор в другой области видимости, а не в области видимости вызова алгоритма.

В качестве потенциального решения вы могли бы подумать о написании локального класса функторов — поскольку C++ всегда поддерживает этот синтаксис. Но это не работает…

Посмотрите на этот код:

Попробуйте скомпилировать его с -std=c++98 , и вы увидите следующую ошибку в GCC:

Если мы посмотрим на N3337 — окончательный вариант C++11, то увидим отдельный раздел для лямбд: [expr.prim.lambda].

Вот базовый пример кода, который также показывает соответствующий объект локального функтора:

Вы также можете проверить CppInsights, который показывает, как компилятор расширяет код:

Посмотрите на этот пример:

Читайте также:

Как подключить вентилятор 12в к сети 220в

В этом примере компилятор преобразует:

Во что-то похожее на это (упрощенная форма):

Некоторые определения, прежде чем мы начнем:

Вычисление лямбда-выражения приводит к временному prvalue. Этот временный объект называется объектом-замыканием (closure object).

Тип лямбда-выражения (который также является типом объекта-замыкания) является уникальным безымянным non-union типом класса, который называется типом замыкания (closure type).

Несколько примеров лямбда-выражений:

Поскольку компилятор генерирует уникальное имя для каждой лямбды, узнать его заранее не представляется возможным.

Поэтому вы не можете написать:

Это приведет к следующей ошибке в GCC:

Читайте также:

Что такое сажевый фильтр на бензине

По умолчанию это встроенный константный метод. Вы можете изменить его, указав mutable после объявления параметров:

Захватив переменную, вы создаете член-копию этой переменной в типе замыкания. Затем внутри тела лямбды вы можете получить к нему доступ.

[&] — захват по ссылке, все переменные в автоматическом хранилище объявлены в области охвата
[=] — захват по значению, значение копируется
[x, & y] — явно захватывает x по значению, а y по ссылке

Вы можете поиграться с полным примером здесь: @Wandbox

Хотя указание [=] или [&] может быть удобно — поскольку оно захватывает все переменные в автоматическом хранилище, более очевидно захватывать переменные явно. Таким образом, компилятор может предупредить вас о нежелательных эффектах (см., например, примечания о глобальных и статических переменных)

И важная цитата:

В приведенном выше примере мы можем изменить значения x и y… но это только копии x и y из прилагаемой области видимости.

Захват глобальных переменных

Если у вас есть глобальное значение, а затем вы используете [=] в лямбде, вы можете подумать, что глобальное значение также захвачено по значению… но это не так.

Поиграть с кодом можно здесь: @Wandbox

Захватываются только переменные в автоматическом хранилище. GCC может даже выдать следующее предупреждение:

Захват статических переменных

Захват статических переменных аналогичен захвату глобальных:

Поиграть с кодом можно здесь: @Wandbox

И снова, предупреждение появится, только если вы явно захватите статическую переменную, поэтому, если вы используете [=] , компилятор вам не поможет.

Захват члена класса

Знаете ли вы, что произойдет после выполнения следующего кода:

Код объявляет объект Baz, а затем вызывает foo() . Обратите внимание, что foo() возвращает лямбду (хранящуюся в std::function ), которая захватывает член класса.

Поскольку мы используем временные объекты, мы не можем быть уверены, что произойдет, при вызове f1 и f2. Это проблема висячих ссылок, которая порождает неопределенное поведение.

Опять же, если вы укажете захват явно ([s]):

Компилятор предотвратит вашу ошибку:

Если у вас есть объект, который может быть только перемещен (например, unique_ptr), то вы не можете поместить его в лямбду в качестве захваченной переменной. Захват по значению не работает, поэтому вы можете захватывать только по ссылке… однако это не передаст его вам во владение, и, вероятно, это не то, что вы хотели.

Если вы захватываете константную переменную, то константность сохраняется:

В C++11 вы можете пропустить trailing возвращаемый тип лямбды, и тогда компилятор выведет его за вас.

Первоначально вывод возвращаемого типа значения был ограничен лямбдами, содержащими один оператор return, но это ограничение было быстро снято, поскольку не было проблем с реализацией более удобной версии.

Таким образом, начиная с C++11, компилятор может вывести тип возвращаемого значения, если все операторы return могут быть преобразованы в один и тот же тип.

Поиграться с кодом можно здесь: @Wandbox

В вышеприведенной лямбде есть два оператора return , но все они указывают на double , поэтому компилятор может вывести тип.

IIFE — Немедленно вызываемые выражения (Immediately Invoked Function Expression)

В наших примерах я определял лямбду, а затем вызвал ее, используя объект замыкания… но ее также можно вызывать немедленно:

Такое выражение может быть полезно при сложной инициализации константных объектов.

Преобразование в указатель на функцию

Другими словами, вы можете преобразовывать лямбды без захватов в указатель на функцию.

Поиграться с кодом можно здесь: @Wandbox

Улучшения в C++14

C++14 добавил два значительных улучшения в лямбда-выражения:

Захваты с инициализатором
Общие лямбды

Вывод типа возвращаемого значения лямбда-выражения был обновлен, чтобы соответствовать правилам автоматического вывода для функций.

Захваты с инициализатором

Короче говоря, мы можем создать новую переменную-член типа замыкания и затем использовать ее внутри лямбда-выражения.

Это может решить несколько проблем, например, с типами, доступными только для перемещения.

Теперь мы можем переместить объект в член типа замыкания:

Другая идея состоит в том, чтобы использовать его как потенциальную технику оптимизации. Вместо того, чтобы вычислять какое-то значение каждый раз, когда мы вызываем лямбду, мы можем вычислить его один раз в инициализаторе:

Инициализатор также можно использовать для захвата переменной-члена. Затем мы можем получить копию переменной-члена и не беспокоиться о висячих ссылках.

Поиграться с кодом можно здесь: @Wandbox

В foo() мы захватываем переменную-член, копируя ее в тип замыкания. Кроме того, мы используем auto для вывода всего метода (ранее, в C++11 мы могли использовать std::function ).

Это эквивалентно использованию объявления шаблона в операторе вызова типа замыкания:

Такая обобщенная лямбда может быть очень полезна, когда трудно вывести тип.

В этой статье мы начали с первых дней лямбда-выражений в C++03 и C++11 и перешли к улучшенной версии в C++14.

Вы увидели, как создавать лямбду, какова основная структура этого выражения, что такое список захвата и многое другое.

В следующей части статьи мы перейдем к C++17 и познакомимся с будущими фичами C++20.

Вторая часть доступна здесь:

В очередном опусе Итана Сигеля резанула фраза

О какой неожиданности может идти речь? Там ведь совершенно шикарная история длиной в 80 лет с яркими открытиями и закрытиями. История про то, как на самом деле делается настоящая наука. История скорее про физиков, чем про физику.

О чём вообще весь сыр-бор?

Первую версию Общей Теории Относительности (ОТО) Альберт Эйнштейн представил публике 25 ноября 1915 года. В оригинале уравнения ОТО Эйнштейна выглядели вот так:

или, в современной записи, вот так:

Для неумеющего в тензоры читателя понятнее уравнение (1) в оригинальной записи Эйнштейна. Там написано, что энергия-импульс материи G равен кривизне пространства R плюс тензор Риччи S. (Этот самый тензор Риччи тоже есть кривизна, только в более другой форме). Сейчас, решая уравнение ОТО, энергию-импульс обычно считают известным, а ищут как раз кривизну. Поэтому в современной записи стороны уравнения поменяли местами. Заодно поменяли буковки: G → T, S → R_μν.

Откуда есть пошла лямбда

Но физика — это вам не математика. Здесь нельзя взять формулу и напихать в неё добавочных слагаемых просто так. Нужно иметь очень веские основания, и теоретические, и экспериментальные.

Хотя ниже вы увидите, насколько мало Эйнштейн знал о Вселенной в те годы, но тогда, в 1916, такие основания у него были. Альберт Германович точно знал, что звёзды не попадали друг на друга и совершенно не собираются этого делать в обозримом будущем. Однако, в ОТО-1915 было только притяжение, которое нужно было чем-то сбалансировать.

Первое физическое толкование смысла лямбды

В такой трактовке ненулевое значение Λ означает, что наша Вселенная искривлена сама по себе, в том числе и при отсутствии какой-либо гравитации. Ну, вот такой нам достался мир. Однако, большинство физиков в это не верят, и считают, что у наблюдаемого искривления должна быть какая-то внутренняя причина. Какая-то неведомая доселе фигня, которую можно открыть.

Первая в том, что мы не можем измерить совсем пустое пространство, потому что просто ничего там не видим. А если там есть что-то, что мы таки видим, то пространство уже не пустое и, значит, уже дополнительно искривлено гравитацией.

Допустим, у нас есть как-то измеренные координаты объектов, плюс пачка фотографий этих объектов в разных ракурсах (снятых из разных точек). Тогда мы можем вычислить кривизну пространства. Например, гравитация Солнца отклоняет пролетающий мимо свет далёких звёзд. Во время солнечных затмений это отклонение можно измерить экспериментально и сравнить с предсказаниями ОТО.

Теперь наоборот: допустим, мы знаем кривизну пространства, и у нас есть пачка фотографий. Тогда, если кривизна достаточно хорошая, без чёрных дыр и т.п. — мы можем вычислить координаты объектов на фото. Именно так работают наши глаза, точнее мозги, когда вычисляют расстояние до объектов по двум фоткам с разных точек.

Поэтому измерить кривизну наблюдаемой Вселенной в целом мы можем только из очень окольных соображений.

Вселенная Фридмана

Meanwhile in Russia, не смотря на войны и революции, над теорией ОТО бился прапорщик (и по совместительству профессор) Александр Александрович Фридман. Он рассмотрел все варианты лямбд и выяснил следующее:

№31 Импеданс полной цепи переменного тока. Сдвиг фаз. Резонанс напряжения.

Рассмотрим последовательно соединенные R, L, C.

При последовательном соединении:

1) Uвх=U0*cosW*t=Ur+Ul+Uc – входное напряжение.

2) I=I0*cos(W*t-фи) – сила тока в цепи.

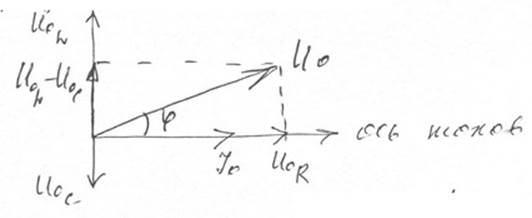
Начертим векторную диаграмму:

Ur0 – совпадает по фазе с силой тока;

Ul0 – опережает на пи/2;

Uc0 – отстает от тока на пи/2.

По теореме Пифагора: (U0)^2=(U0r)^2+(U0l-U0c)^2

Сократив обе части уравнения на (I0)^2 получим выражение для полного сопротивления (Z):

Z=квадратный корень из (R^2+(W*L-1/W*c)^2) – импеданс.

Если сопротивление катушки Xl= W*L равно сопротивлению конденсатора Xc=1/W*c, то полное сопротивление Z=R; по закону Ома Iрез=U0/Z=U0/R (Iрез – резонансный ток) – сила тока резко возрастает – РЕЗОНАНС. При этом Ul=Uc>>U0 – резонанс напряжений. Это возможно, т.к. Ul и Uc сдвинуты по фазе между собой на пи:

При этом на резисторе R выделяется максимальное количество теплоты:

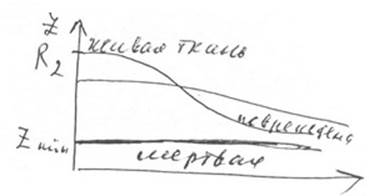
№32 Импенданс тканей организма. Эквивалентная Электрическая схема. Оценка жизнеспособности тканей и органов но частотной зависимости к углу сдвига фаз.

Ткани организма проводят как постоянный так и переменный ток. Биологическая мембрана а значит и весь организм обладает емкостным сопротивлением, т.к. обладают емкостью, т.е. способны

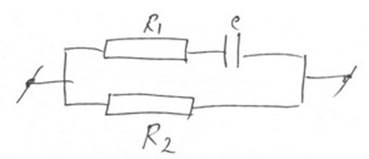
накапливать заряд. При пропускании через живые ткани переменного тока наблюдается отставание напряжения от тока. Омические емкостные свойства биологических тканей можно моделировать используя эквивалентные электрические схемы, при любых частотах зависимость сдвига фаз и импенданса от частоты выполняется для схемы

1/Zв2=1/Rв2+1/корень(R1 в2+1/Wв2*Св2)!, где Z-полное сопротивление данной цепи, с — ёмкость.

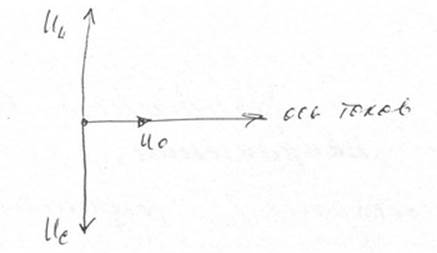
При малых частотах: Z=R2 При больших частотах: Zmin=(R1*R2)/(R1+R2).

Графическое изображение зависимости импенданса живой ткани от частоты переменного тока.

Сдвиг фаз между током и напряжением tg фи = R/Xc=RWC (1).

Частотная зависимость сдвига фаз живой ткани. При отмирании ткани натрий-калиевый канал биологических мембран разрушается, цитоплазма

клетки (проводник) соединяется с межклеточной

жидкостью(проводник) и емкостные свойства ткани уменьшаются, а это значит, что и импенданс (Z) и сдвиг фаз (фи) меньше зависят от частоты. Мёртвая ткань обладает лишь омическим сопротивлением (R), и не зависит от частоты. Диагностический метод, основанный на регистрации изменения импенданса тканей и сдвига фаз называется РЕОГРАФИЕЙ.

Что означает лямбда в отношении лямбда ст c v

Вопрос по физике:

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

02.09.2018 22:33
Физика
remove_red_eye 18575
thumb_up 5

Ответы и объяснения 1

03.09.2018 22:52
thumb_up 26

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
Использовать мат — это неуважительно по отношению к пользователям;
Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Физика.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Физика — область естествознания: естественная наука о простейших и вместе с тем наиболее общих законах природы, о материи, её структуре и движении.

Лямбды: от C++11 до C++20. Часть 1

Добрый день, друзья. Сегодня мы подготовили для вас перевод первой части статьи «Лямбды: от C++11 до C++20». Публикация данного материала приурочена к запуску курса «Разработчик C++», который стартует уже завтра.

Вступление

На одном из местных собраний C++ User Group у нас был живой сеанс программирования по «истории» лямбда-выражений. Беседу вел эксперт по С++ Томас Каминский (Tomasz Kamiński) (см. профиль Томаса в Linkedin). Вот это событие:

Я решил взять код у Томаса (с его разрешения!), описать его и создать отдельную статью.

«Лямбды» в C++03

Посмотрите на этот код:

Попробуйте скомпилировать его с -std=c++98 , и вы увидите следующую ошибку в GCC:

Если мы посмотрим на N3337 — окончательный вариант C++11, то увидим отдельный раздел для лямбд: [expr.prim.lambda].

Далее к C++11

Я думаю, что лямбды были добавлены в язык с умом. Они используют новый синтаксис, но затем компилятор «расширяет» его до реального класса. Таким образом, у нас есть все преимущества (а иногда и недостатки) реального строго типизированного языка.

Вот базовый пример кода, который также показывает соответствующий объект локального функтора:

Вы также можете проверить CppInsights, который показывает, как компилятор расширяет код:

Посмотрите на этот пример:

В этом примере компилятор преобразует:

Во что-то похожее на это (упрощенная форма):

Некоторые определения, прежде чем мы начнем:

Несколько примеров лямбда-выражений:

Поэтому вы не можете написать:

Это приведет к следующей ошибке в GCC:

Оператор вызова

Код, который вы помещаете в тело лямбды, «транслируется» в код operator() соответствующего типа замыкания.

Хотя константный метод не является «проблемой» для лямбды без пустого списка захвата… он имеет значение, когда вы хотите что-то захватить.

[] не только вводит лямбду, но также содержит список захваченных переменных. Это называется «список захвата».

[&] — захват по ссылке, все переменные в автоматическом хранилище объявлены в области охвата
[=] — захват по значению, значение копируется
[x, & y] — явно захватывает x по значению, а y по ссылке

Вы можете поиграться с полным примером здесь: @Wandbox

Вы также можете прочитать больше в пункте 31 «Эффективного современного C++» Скотта Мейерса: «Избегайте режимов захвата по умолчанию».

И важная цитата:

Захват глобальных переменных

Поиграть с кодом можно здесь: @Wandbox

Захватываются только переменные в автоматическом хранилище. GCC может даже выдать следующее предупреждение:

Захват статических переменных

Захват статических переменных аналогичен захвату глобальных:

Поиграть с кодом можно здесь: @Wandbox

Захват члена класса

Знаете ли вы, что произойдет после выполнения следующего кода:

Опять же, если вы укажете захват явно ([s]):

Компилятор предотвратит вашу ошибку:

Move-able-only объекты

Сохранение констант

Если вы захватываете константную переменную, то константность сохраняется:

Возвращаемый тип

В C++11 вы можете пропустить trailing возвращаемый тип лямбды, и тогда компилятор выведет его за вас.

Поиграться с кодом можно здесь: @Wandbox

IIFE — Немедленно вызываемые выражения (Immediately Invoked Function Expression)

Такое выражение может быть полезно при сложной инициализации константных объектов.

Преобразование в указатель на функцию

Другими словами, вы можете преобразовывать лямбды без захватов в указатель на функцию.

Поиграться с кодом можно здесь: @Wandbox

Улучшения в C++14

C++14 добавил два значительных улучшения в лямбда-выражения:

Захваты с инициализатором
Общие лямбды

Возвращаемый тип

Захваты с инициализатором

Это может решить несколько проблем, например, с типами, доступными только для перемещения.

Перемещение

Теперь мы можем переместить объект в член типа замыкания:

Оптимизация

Захват переменной-члена

Поиграться с кодом можно здесь: @Wandbox

Обобщенные лямбда-выражения

Это эквивалентно использованию объявления шаблона в операторе вызова типа замыкания:

Такая обобщенная лямбда может быть очень полезна, когда трудно вывести тип.

В этой статье мы начали с первых дней лямбда-выражений в C++03 и C++11 и перешли к улучшенной версии в C++14.

В следующей части статьи мы перейдем к C++17 и познакомимся с будущими фичами C++20.

Вторая часть доступна здесь:

Ждем ваши комментарии и приглашаем всех заинтересованных на курс «Разработчик С++».

Что обозначает лямбда в отношении лямбда ct c v

Сомнительная заправка, плохой бензин, «чек» на панели — стандартный и быстрый путь к замене кислородного датчика. Про лямбда-зонд слышали многие автомобилисты, но мало кто разбирался, за что именно он отвечает и почему так легко выходит из строя. Рассказываем про датчик кислорода — «обоняние» двигателя.

Лямбда и стехиометрия двигателя

Название датчика происходит от греческой буквы λ (лямбда), которая обозначает коэффициент избытка воздуха в топливно-воздушной смеси. Для полного сгорания смеси соотношение воздуха с топливом должно быть 14,7:1 (λ=1). Такой состав топливно-воздушной смеси называют стехиометрическим — идеальным с точки зрения химической реакции: топливо и кислород в воздухе будут полностью израсходованы в процессе горения. При этом двигатель произведёт минимум токсичных выбросов, а соотношение мощности и расхода топлива будет оптимальным.

Если лямбда будет <1 (недостаток воздуха), смесь станет обогащённой; при лямбде>1 (избыток воздуха) смесь называют обеднённой. Чересчур богатая смесь — это повышенный расход топлива и более токсичный выхлоп, а слишком бедная смесь грозит потерей мощности и нестабильной работой двигателя.

Из графика видно, что при λ=1 мощность двигателя не пиковая, а расход топлива не минимален — это лишь оптимальный баланс между ними. Наибольшую мощность мотор развивает на слегка обогащённой смеси, но расход топлива при этом возрастает. А максимальная топливная эффективность достигается на слегка обеднённой смеси, но ценой падения мощности. Поэтому задача ЭБУ (электронного блока управления) двигателя — корректировать топливно-воздушную смесь исходя из ситуации: обогащать её при холодном пуске или резком ускорении, и обеднять при равномерном движении, добиваясь оптимальной работы мотора во всех режимах. Для этого блок управления ориентируется на показания датчика кислорода.

Зачем нужен кислородный датчик

Датчиков в современном двигателе великое множество . С помощью различных сенсоров ЭБУ замеряет температуру забортного воздуха и его поток, «видит» положение дроссельной заслонки, отслеживает детонацию и положение коленвала — словом, внимательно следит за воздухом «на входе» и показателями работы мотора, регулируя подачу топлива для создания оптимальной смеси в цилиндрах.

Лямбда-зонд показывает, что же получилось «на выходе», замеряя количество кислорода в выхлопных газах. Другими словами, кислородный датчик определяет, оптимально ли работает мотор, соответствуют ли расчёты ЭБУ реальной картине и нужно ли вносить в них поправки. Основываясь на данных с лямбда-зонда, ЭБУ вносит соответствующие коррекции в работу двигателя и подготовку топливно-воздушной смеси.

Где находится кислородный датчик

Датчик кислорода установлен в выпускном коллекторе или приёмной трубе глушителя двигателя, замеряя, сколько несгоревшего кислорода находится в выхлопных газах. На многих автомобилях есть ещё один лямбда-зонд, расположенный после каталитического нейтрализатора выхлопа — для контроля его работы.

Если у двигателя две головки блока (V-образники, «оппозитники»), то удваивается количество выпускных коллекторов и катализаторов, а значит и лямбда-зондов — у современной машины может быть и 4 кислородных датчика.

Устройство кислородного датчика

Классический лямбда-зонд порогового типа — узкополосный — работает по принципу гальванического элемента. Внутри него находится твёрдый электролит — керамика из диоксида циркония, поэтому такие датчики часто называют циркониевыми. Поверх керамики напылены токопроводящие пористые электроды из платины. Будучи погружённым в выхлопные газы, датчик реагирует на разницу между уровнем кислорода в них и в атмосферном воздухе, вырабатывая на выходе напряжение, которое считывает ЭБУ.

Циркониевый элемент лямбда-зонда приобретает проводимость и начинает работать только после прогрева до температуры 300 °C. До этого ЭБУ двигателя действует «вслепую» согласно топливной карте, без обратной связи от кислородного датчика, что повышает расход топлива при прогреве двигателя и количество вредных выбросов. Чтобы быстрее задействовать лямбда-зонд, ему добавляют принудительный электрический подогрев. Кислородные датчики с подогревом внешне отличаются увеличенным количеством проводов: у них 3–4 жилы против 1–2 у обычных датчиков.

В названии узкополосного датчика кроется его недостаток — он способен замерять количество кислорода в выхлопе в достаточно узком диапазоне. ЭБУ может корректировать смесь по его показаниям только в некоторых режимах работы мотора (холостой ход, движение с постоянной скоростью), что не отвечает современным требованиям по экономичности и экологичности двигателей. Для более точных замеров в широком диапазоне используют широкополосный лямбда-зонд (A/F-сенсор), который также называют датчиком соотношения «воздух-топливо» (Air/Fuel Sensor). Обычно к нему подходят 5–6 проводов, хотя бывают и исключения.

Внешне «широкополосник» похож на обычный датчик кислорода, но внутри есть отличия. Благодаря специальным накачивающим ячейкам эталонный лямбда-коэффициент газового содержимого датчика всегда равен 1, и генерируемое им напряжение постоянно. А вот ток меняется в зависимости от количества кислорода в выхлопных газах, и ЭБУ двигателя считывает его в реальном времени. Это позволяет электронике быстрее и точнее корректировать смесь, добиваясь её полного сгорания в цилиндрах.

Почему до сих пор производят узкополосные датчики? Во-первых, для старых автомобилей, где A/F-сенсоры не применялись. Во-вторых, из-за особенностей «широкополосника» его нельзя устанавливать после катализатора, где он быстро выходит из строя. А контролировать работу катализатора как-то надо. Поэтому в современных двигателях ставят два лямбда-зонда разного типа: широкополосный (управляющий) — в районе выпускного коллектора, а узкополосный (диагностический) — после катализатора.

Причины и признаки неисправности лямбда-зонда

Основная причина поломок кислородных датчиков — некачественный бензин: свинец и ферроценовые присадки оседают на чувствительном элементе датчика, выводя его из строя. На состояние лямбда-зонда влияет и нестабильная работа двигателя: при пропусках зажигания от старых свечей или пробитых катушек несгоревшая смесь попадает в выхлопную систему, где догорает, выжигая и катализатор, и датчики кислорода. Приговорить датчик также может попадание в цилиндры антифриза или масла.

Самый очевидный признак неисправности лямбда-зонда — индикатор Check Engine на приборной панели. Считав код ошибки с помощью сканера или самодиагностики, можно проверить, какой именно датчик вышел из строя, если их несколько. Иногда всё дело в повреждённой проводке датчика — с проверки цепи и стоит начать поиск поломки.

Но далеко не всегда проблемный лямбда-зонд зажигает «Чек»: иногда он не ломается полностью, а медленно умирает, давая при этом ложные показания, из-за чего ЭБУ двигателя неверно корректирует состав смеси. В этом случае нужно ориентироваться на косвенные признаки — ухудшение работы двигателя.

Проблемы с датчиком кислорода нарушают всю систему обратной связи и лямбда-коррекции, вызывая целый букет неисправностей. Прежде всего, это увеличение расхода топлива и токсичности выхлопа, снижение мощности и нестабильный холостой ход. Если вовремя не заменить лямбда-зонд, следом выйдет из строя каталитический нейтрализатор, осыпавшись из-за перегрева от обогащённой смеси.

Универсальные кислородные датчики

Цена на оригинальные датчики кислорода вряд ли обрадует автомобилистов, но все лямбда-зонды работают по единому принципу, что позволяет без труда подобрать замену. Главное, чтобы соответствовал типа датчика (широкополосный/узкополосный), количество проводов и резьбовая часть. В продаже есть универсальные кислородные датчики без разъёма, которые можно использовать на десятках моделей автомобилей — подобрать и купить лямбда-зонд не составляет проблемы.

Чтобы избежать проблем с кислородными датчиками, следите за состоянием двигателя, заправляйтесь качественным топливом и регулярно выполняйте компьютерную диагностику, которая позволит выявить неисправности на ранней стадии.

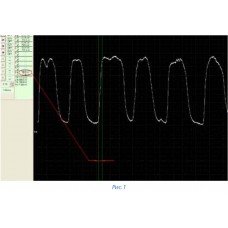
Для случая исправного датчика на прогретом двигателе в режиме холостого хода на экране прибора будут видны равномерные, близкие к синусоиде колебания с частотой 1…5 Гц. с минимальным значением сигнала 0,1 вольт, максимальным 0,9 вольт, вокруг среднего значения 0,45 вольт с длительностью фронтов сигнала не более 250 миллисекунд. Такой же сигнал (только с большей частотой) должен наблюдаться и при повышенных оборотах двигателя. Все вышесказанное относится к датчику, установленному перед катализатором. Если у циркониевого датчика фронт сигнала превышает 350 мсек., сигнал низкого уровня более 0,2 вольт, а сигнал высокого уровня менее 0,8 вольт — есть повод задуматься о предстоящей замене датчика.

Все подсоединяем (разьем позволяет подсоединяться просто подоткнув проводки, использовал медные одножильные с толщиной жилы 0,5), прогреваем двигатель (пишут до включения вентилляторов), измеряем на холостом ходу (для сведения), а все основные измерения проводим при 2000 об/мин (т.к. помошника небыло я сделал из проволочки петельку, накинул ее на усик тросика привода дроссельной заслонки, заслонку повернул на угол при котором обороты были 2000 по тахометру авто и проволочку привязал к подходящей железке неподалеку — зафиксировал обороты на 2000 без моего участия, чтобы руки и ноги освободить)

Т.к. практического опыта нет то сравнивал все с теорией (методикой) с сайта NGK (она совпадает с прочими обнаруженными в интернете почти по всем) — если датчик живой или не совсем мертвый то будут колебания типа синусоиды. Смотрим амплитуду — на живом и прогретом, согласно требований производителя, колебаться должно от 0,1В до 0,9В. Смотрим как по времени раскладывается — пишут что при 2000об/мин время между двумя идущими друг за другом горбиками или ямками (если не путаю это у нас период зовется) не должно быть более 0,7-1сек. Картинку того что должно быть в теории я приводил чуть раньше (взято с сайта NGK/NTK).

Мной опробован датчик NGK/NTK OZA333-H4 (или код 0137) — РАЗЬЕМ РОДНОЙ, НИЧЕГО ДЕЛАТЬ НЕ НАДО

Лямбда-исчисление — это формальная система в математической логике для выражения подсчетов на основе абстракции и применения функций с использованием привязки и подстановки переменных. Это универсальная модель, которую можно применять для проектирования любой машины Тьюринга. Впервые введена лямбда-исчисления Черчем, известным математиком, в 1930-х годах.

Система состоит из построения лямбда-членов и выполнения над ними операций сокращения.

Пояснения и приложения

Греческая буква lambda (λ) используется в лямбда-выражениях и лямбда-терминах для обозначения связывания переменной в функции.

Лямбда-исчисление может быть нетипизировано или типизировано. В первом варианте функции могут быть применены только в том случае, если они способны принимать данные этого типа. Типизированные лямбда-исчисления слабее, могут выражать меньшее значение. Но, с другой стороны, они позволяют доказывать больше вещей.

Одной из причин того, что существует много разных типов — это желание ученых сделать больше, не отказываясь от возможности доказывать сильные теоремы лямбда-исчислений.

Система находит применение во многих различных областях математики, философии, лингвистики, и компьютерных наук. В первую очередь, лямбда-исчисления — это расчет, который сыграл важную роль в развитии теории языков программирования. Именно стили функционального создания реализуют системы. Они также являются актуальной темой исследований в теории этих категорий.

Для чайников

Лямбда-исчисление была введена математиком Алонзо Черчем в 1930-х годах в рамках исследования основ науки. Первоначальная система была показана как логически несовместимая в 1935 году, когда Стивен Клин и Дж. Б. Россер разработали парадокс Клини-Россера.

В последствии, в 1936 году Черч выделил и опубликовал только ту часть, которая имеет отношение к расчетам, то, что сейчас называется нетипизированным лямбда-исчислением. В 1940 он также представил более слабую, но логически непротиворечивую теорию, известную как система простого типа. В свое работе он объясняет всю теорию простым языком, поэтому, можно сказать, что Черч опубликовал лямбду исчисления для чайников.

До 1960-х годов, когда выяснилось его отношение к языкам программирования, λ стала лишь формализмом. Благодаря применениям Ричарда Монтегю и других лингвистов в семантике естественного языка, исчисление стало занимать почетное место как в лингвистике, так и в информатике.

Происхождение символа

Лямбда не обозначает слово или аббревиатуру, она возникла, благодаря ссылки в «Принципиальной математике» Рассела, за которой следуют два типографских изменения. Пример обозначения: для функции f с f (y) = 2y + 1 равно 2ŷ + 1. И здесь используется символ каретки («шляпа») над y для пометки входной переменной.

Церковь изначально намеревалась использовать аналогичные символы, но наборщики не смогли разместить символ «шляпа» над буквами. Поэтому вместо этого они напечатали его изначально как «/y.2y+1». В следующем эпизоде редактирования наборщики заменили «/ » на визуально похожий символ.

Введение в лямбда исчисление

Система состоит из языка терминов, которые выбираются определенным формальным синтаксисом, и набора правил преобразования, которые позволяют манипулировать ими. Последний пункт можно рассматривать как эквациональную теорию или как операционное определение.

Все функции в лямбда-исчислении являются анонимными, то есть не имеющими имен. Они принимают только одну входную переменную, при этом каррирование используется для реализации графиков с несколькими непостоянными.

Лямбда-термины

Синтаксис исчисления определяет некоторые выражения как допустимые, а другие — как недействительные. Также, как различные строки символов являются допустимыми программами на Си, а какие-то — нет. Действительное выражение лямбда-исчисления называется «лямбда-термином».

Следующие три правила дают индуктивное определение, которое можно применять для построения всех синтаксически допустимых понятий:

Переменная x сама по себе является действительным лямбда-термином:

если T это ЛТ, и x непостоянная, то (lambda xt) называется абстракцией.
если T, а также s понятия, то (TS) называется приложением.

Ничто другое не является лямбда-термином. Таким образом, понятие действительно тогда и только тогда, когда оно может быть получено повторным применением этих трех правил. Тем не менее некоторые скобки могут быть опущены в соответствии с другими критериями.

Определение

Лямбда-выражения состоят из:

переменных v 1, v 2. v n.
символов абстракции ‘λ’ и точки ‘.’
скобок ().

Множество Λ, может быть определено индуктивно:

Если x переменная, то x ∈ Λ;
x непостоянная и M ∈ Λ, то (λx.M) ∈ Λ;
M, N ∈ Λ, то (MN) ∈ Λ.

Обозначение

Чтобы сохранить нотацию лямбда-выражений в незагроможденном виде, обычно применяются следующие соглашения:

Внешние скобки опущены: MN вместо (MN).
Предполагается, что приложения остаются ассоциативными: взамен ((MN) P) можно написать MNP.
Тело абстракции простирается дальше вправо: λx.MN означает λx. (MN), а не (λx.M) N.
Сокращается последовательность абстракций: λx.λy.λz.N можно λxyz.N.

Свободные и связанные переменные

Оператор λ соединяет свою непостоянную, где бы он ни находился в теле абстракции. Переменные, попадающие в область, называются связанными. В выражении λ x. М, часть λ х часто называют связующим. Как бы намекая, что переменные становятся группой с добавлением Х х к М. Все остальные неустойчивые называются свободными.

Например, в выражении λ y. х х у, у — связанная непостоянная, а х — свободная. И также стоит обратить внимание, что переменная сгруппирована своей «ближайшей» абстракцией. В следующем примере решение лямбда-исчисления представлено единственным вхождением x, которое связано второй составляющей:

Множество свободных переменных M обозначается как FV (M) и определяется рекурсией по структуре терминов следующим образом:

FV (x) = , где x — переменная.
FV (λx.M) = FV (M) .
FV (MN) = FV (M) ∪ FV (N).

Формула, которая не содержит свободных переменных, называется закрытой. Замкнутые лямбда-выражения также известны как комбинаторы и эквивалентны терминам в комбинаторной логике.

Сокращение

Значение лямбда-выражений определяется тем, как они могут быть сокращены.

Существует три вида урезания:

α-преобразование: изменение связанных переменных (альфа).
β-редукция: применение функций к своим аргументам (бета).
η-преобразование: охватывает понятие экстенсиональности.

Здесь речь также идет о полученных эквивалентностях: два выражения являются β-эквивалентными, если они могут быть β-преобразованы в одно и то же составляющее, а α / η-эквивалентность определяется аналогично.

Термин redex, сокращение от приводимого оборота, относится к подтемам, которые могут быть сокращены одним из правил. Лямбда исчисление для чайников, примеры:

(λ x.M) N является бета-редексом в выражении замены N на x в M. Составляющее, к которому сводится редекс, называется его редуктом. Редукция (λ x.M) N есть M [x: = N].

Если x не является свободной в M, λ х. М х также ет-REDEX с регулятором М.

α-преобразование

Альфа-переименования позволяют изменять имена связанных переменных. Например, λ x. х может дать λ у. у. Термины, которые отличаются только альфа-преобразованием, называются α-эквивалентными. Часто при использовании лямбда-исчисления α-эквивалентные считаются взаимными.

Точные правила для альфа-преобразования не совсем тривиальны. Во-первых, при данной абстракции переименовываются только те переменные, которые связаны с одной и той же системой. Например, альфа-преобразование λ x.λ x. x может привести к λ y.λ x. х, но это может не ввергнуть к λy.λx.y Последний имеет иной смысл, чем оригинал. Это аналогично понятию программирования затенения переменных.

Во-вторых, альфа-преобразование невозможно, если оно приведет к захвату непостоянной другой абстракцией. Например, если заменить x на y в λ x.λ y. x, то можно получить λ y.λ y. у, что совсем не то же самое.

В языках программирования со статической областью видимости альфа-преобразование можно использовать для упрощения разрешения имен. При этом следя за тем, чтобы понятие переменной не маскировало обозначение в содержащей области.

В нотации индекса Де Брюйна любые два альфа-эквивалентных термина синтаксически идентичны.

Замена

Изменения, написанные Е [V: = R], представляют собой процесс замещения всех свободных вхождений переменной V в выражении Е с оборотом R. Подстановка в терминах λ определяется лямбдой исчисления рекурсии по структуре понятий следующим образом (примечание: x и y — только переменные, а M и N — любое λ-выражение).

y [x: = N] ≡ y, если x ≠ y

(M 1 M 2) [x: = N] ≡ (M 1 [x: = N]) (M 2 [x: = N])

(λ y.M) [x: = N] y λ y. (M [x: = N]), если x ≠ y, при условии, что y ∉ FV (N).

Для подстановки в лямбда-абстракцию иногда необходимо α-преобразовать выражение. Например, неверно, чтобы (λ x. Y) [y: = x] приводило к (λ x. X), потому что замещенный x должен был быть свободным, но в итоге был связанным. Правильная замена в этом случае (λ z. X) с точностью до α-эквивалентности. Стоит обратить внимание, что замещение определяется однозначно с верностью до лямбды.

β-редукция

Бета-редукция отражает идею применения функции. Бета-восстановительный определяется в терминах замещения: ((X V. E) Е ‘) является Е [V: = Е’].

Например, предполагая некоторое кодирование 2, 7, ×, имеется следующее β-уменьшение: ((λ n. N × 2) 7) → 7 × 2.

Бета-редукция может рассматриваться как то же самое, что и концепция локальной сводимости при естественной дедукции через изоморфизм Карри – Ховарда.

η-преобразование

Эта-конверсия выражает идею экстенсиональности, которая в этом контексте заключается в том, что две функции равны тогда, когда они дают одинаковый результат для всех аргументов. Эта конвертация обменивает между λ x. (F x) и f всякий раз, когда x не кажется свободным в f.

Данное действие может рассматриваться как то же самое, что и концепция локальной полноты в естественной дедукции через изоморфизм Карри – Ховарда.

Нормальные формы и слияние

Для нетипизированного лямбда-исчисления β-редукция как правило переписывания не является ни сильно нормализующей, ни слабо.

Тем не менее можно показать, что β-редукция сливается при работе до α-преобразования (т. е. можно считать две нормальные формы равными, если возможно α-преобразование одной в другую).

Поэтому и сильно нормализующие члены, и слабо налаживающие понятия имеют единственную нормальную форму. Для первых терминов любая стратегия сокращения гарантированно приведет к типичной конфигурации. Тогда как для слабо нормализующих условий некоторые стратегии сокращения могут не найти ее.

Дополнительные методы программирования

Существует большое количество идиом создания для лямбда-исчисления. Многие из них были первоначально разработаны в контексте использования систем в качестве основы для семантики языка программирования, эффективно применяя их в качестве создания низкого уровня. Поскольку некоторые стили включают лямбда-исчисление (или что-то очень похожее) в качестве фрагмента, эти методы также находят применение в практическом создании, но затем могут восприниматься как неясные или чужие.

Именованные константы

В лямбда-исчислении библиотека принимает форму набора ранее определенных функций, в которой термины являются просто конкретными константами. Чистое исчисление не имеет понятия именованных неизменных, поскольку все атомные лямбда-термины являются переменными. Но их также можно имитировать, выделив непостоянную в качестве имени константы, используя лямбда-абстракцию для связывания этой изменчивой в основной части, и применить эту абстракцию к намеченному определению. Таким образом, если использовать f для обозначения M в N, можно сказать,

Авторы часто вводят синтаксическое понятие, такое как let, чтобы разрешить писать все в более интуитивном порядке.

Объединяя в цепочку такие определения, можно написать «программу» лямбда-исчисления как ноль или более дефиниций функций, за которыми следует один лямбда-член, используя те определения, которые составляют основную часть программы.

Заметным ограничением этого let является то, что имя f не определено в M, поскольку M находится вне области привязки лямбда-абстракции f. Это означает, что атрибут рекурсивной функции не может использоваться как M с let. Более продвинутая синтаксическая конструкция letrec, которая позволяет писать рекурсивные определения функций в этом стиле, вместо этого дополнительно использует комбинаторы с фиксированной точкой.

Печатные аналоги

Данный тип является типизированным формализмом, который использует символ для обозначения анонимной функции абстракция. В этом контексте типы обычно являются объектами синтаксической природы, которые присваиваются лямбда-терминам. Точная натура зависит от рассматриваемого исчисления. С определенной точки зрения, типизированные ЛИ можно рассматривать как уточнения нетипизированного ЛИ. Но с другой стороны, их также можно считать более фундаментальной теорией, а нетипизированное лямбда-исчисление — особым случаем только с одним типом.

Типизированные ЛИ являются основополагающими языками программирования и основой функциональных, таких как ML и Haskell. И, более косвенно, императивных стилей создания. Типизированные лямбда-исчисления играют важную роль в разработке систем типов для языков программирования. Здесь типизируемость обычно захватывает желательные свойства программы, например, она не вызовет нарушения доступа к памяти.

Типизированные лямбда-исчисления тесно связаны с математической логикой и теорией доказательств через изоморфизм Карри – Говарда, и их можно рассматривать как внутренний язык классов категорий, например, который просто является стилем декартовых замкнутых.

В C++ 11 и более поздних версиях лямбда-выражение, часто называемое лямбда– — это удобный способ определения объекта анонимной функции ( замыкания) непосредственно в расположении, где оно вызывается или передается в качестве аргумента функции. Обычно лямбда-выражения используются для инкапсуляции нескольких строк кода, передаваемых алгоритмам или асинхронным методам. В этой статье приводится определение лямбда-выражений, их сравнение с другими методами программирования, описание их преимуществ и простой пример.

См. также

Структура лямбда-выражения

В стандарте ISO C++ демонстрируется простое лямбда-выражение, передаваемое функции std::sort() в качестве третьего аргумента:

На следующем рисунке показана структура лямбда-выражения:

предложение Capture (также известное как оператор лямбда-выражения в спецификации C++).

список параметров Используемых. (Также называется лямбда-объявлением)

изменяемая спецификация Используемых.

Спецификация Exception Используемых.

замыкающий-возвращаемый тип Используемых.

Предложение фиксации

Лямбда-выражение может добавлять новые переменные в тексте (в C++ 14), а также получать доступ к переменным из окружающей области или записывать их. Лямбда-выражение начинается с предложения Capture (лямбда- знаком в стандартном синтаксисе), который указывает, какие переменные захватываются и является ли захват значением или ссылкой. Доступ к переменным с префиксом с амперсандом ( & ) осуществляется по ссылке, а к переменным без префикса — по значению.

Пустое предложение фиксации ( [ ] ) показывает, что тело лямбда-выражения не осуществляет доступ к переменным во внешней области видимости.

Можно использовать режим записи по умолчанию (захват по умолчанию в стандартном синтаксисе), чтобы указать, как записывать все внешние переменные, на которые имеются ссылки в лямбда-выражении: означает, что [&] все переменные, на которые вы ссылаетесь, записываются по ссылке, а [=] значит, они записываются по значению. Можно сначала использовать режим фиксации по умолчанию, а затем применить для определенных переменных другой режим. Например, если тело лямбда-выражения осуществляет доступ к внешней переменной total по ссылке, а к внешней переменной factor по значению, следующие предложения фиксации эквивалентны:

При использовании записи по умолчанию фиксируются только переменные, указанные в лямбда-выражении.

Если предложение Capture включает запись по умолчанию & , то identifier в capture предложении записи нет возможности использовать форму & identifier . Аналогично, если предложение Capture включает запись-Default = , то ни одно capture из этого предложения записи не может иметь форму = identifier . Идентификатор или this не может использоваться в предложении Capture более одного раза. В следующем фрагменте кода приводится несколько примеров.

Захват, за которым следует многоточие, — это расширение пакета, как показано в следующем примере шаблона Variadic :

Чтобы использовать лямбда-выражения в теле метода класса, передайте this указатель в предложение Capture, чтобы предоставить доступ к методам и членам данных включающего класса.

Visual Studio 2017 версии 15,3 и более поздних версий (доступно с /std: c++ 17): this указатель может быть захвачен значением путем указания *this в предложении Capture. Захват по значению означает, что весь замыкание, которое является объектом анонимной функции, енкапулатес лямбда-выражение, копируется в каждый сайт вызова, где вызывается лямбда. Захват по значению полезен, когда лямбда-выражение будет выполняться в параллельных или асинхронных операциях, особенно на определенных аппаратных архитектурах, таких как NUMA.

Пример, демонстрирующий использование лямбда-выражений с методами класса, см. в разделе “пример: использование лямбда-выражения в методе” в примерах лямбда-выражений.

При использовании предложения фиксации рекомендуется помнить об этих важных аспектах, особенно при использовании лямбда-выражений с многопоточностью:

Фиксацию ссылок можно использовать для изменения переменных снаружи, тогда как фиксацию значений нельзя. ( mutable позволяет изменять копии, но не оригиналы.)

Фиксация ссылок отражает изменение переменных снаружи, тогда как фиксация значений — нет.

Фиксация ссылки вводит зависимость от времени существования, тогда как фиксация значения не обладает зависимостями от времени существования. Это особенно важно в случае асинхронного использования лямбда-выражений. Если в асинхронном лямбда-выражении по ссылке фиксируется локальная переменная, вполне вероятно, что к моменту его вызова она станет недоступной, что вызовет исключение нарушения прав доступа во время выполнения.

Обобщенная фиксация (C++14)

В C++14 вы можете объявлять и инициализировать новые переменные в предложении фиксации. Для этого не требуется, чтобы эти переменные существовали во внешней области видимости лямбда-функции. Инициализация может быть выражена в качестве любого произвольного выражения. Тип новой переменной определяется типом, который создается выражением. Одно из преимуществ этой возможности заключается в том, что в C++14 таким образом можно фиксировать переменные из окружающей области видимости, доступные только для перемещения (например std::unique_ptr), и использовать их в лямбда-выражении.

Список параметров

В дополнение к возможности фиксации переменных, лямбда-выражения могут принимать входные параметры. Список параметров (лямбда-декларатор в стандартном синтаксисе) является необязательным и в большинстве аспектов напоминает список параметров для функции.

В C++ 14, если тип параметра является универсальным, можно использовать auto ключевое слово в качестве спецификатора типа. Это отдает компилятору команду создать оператор вызова функции в качестве шаблона. Каждый экземпляр auto в списке параметров эквивалентен отдельному параметру типа.

Лямбда-выражение может принимать другое лямбда-выражение в качестве своего аргумента. Дополнительные сведения см. в разделе “лямбда-выражения более высокого порядка” статьи Примеры лямбда-выражений.

Поскольку список параметров является необязательным, можно опустить пустые скобки, если аргументы не передаются в лямбда-выражение, а лямбда-декларатор не содержит спецификацию Exception, завершающего-Return-Type или mutable .

Отключаемая спецификация

Как правило, оператор вызова функции лямбда-выражения является константой по значению, но использование mutable ключевого слова отменяет это. Он не создает изменяемые элементы данных. Отключаемая спецификация позволяет телу лямбда-выражения изменять переменные, захваченные по значению. В некоторых примерах, приведенных далее в этой статье, показано, как использовать mutable .

Спецификация исключений

Можно использовать noexcept спецификацию исключения, чтобы указать, что лямбда-выражение не создает исключений. Как и в случае с обычными функциями, компилятор Microsoft C++ создает предупреждение C4297 , если лямбда-выражение объявляет noexcept спецификацию исключения, а тело лямбда-выражения создает исключение, как показано ниже:

Дополнительные сведения см. в разделе спецификации исключений (throw).

Тип возвращаемых данных

Возвращаемый тип лямбда-выражения выводится автоматически. Не обязательно использовать auto ключевое слово, если не указан завершающий возвращаемый тип. Замыкающий возвращаемый тип напоминает часть возвращаемого типа в обычном методе или функции. Однако возвращаемый тип должен следовать за списком параметров -> . перед возвращаемым типом необходимо включить ключевое слово замыкающего возвращаемого типа.

Можно опустить часть возвращаемого типа лямбда-выражения, если тело лямбда-выражения содержит только один оператор return или лямбда-выражение не возвращает значение. Если тело лямбда-выражения содержит один оператор return, компилятор выводит тип возвращаемого значения из типа возвращаемого выражения. В противном случае компилятор выводит возвращаемый тип в значение void . Рассмотрим следующие примеры кода, иллюстрирующие этот принцип.

Лямбда-выражение может создавать другое лямбда-выражение в качестве своего возвращаемого значения. Дополнительные сведения см. в разделе “лямбда-выражения более высокого порядка” в примерах лямбда-выражений.

Тело лямбда-выражения

Тело лямбда-выражения (составной оператор в стандартном синтаксисе) в лямбда-выражении может содержать все, что может содержать тело обычного метода или функции. Тело обычной функции и лямбда-выражения может осуществлять доступ к следующим типам переменных:

Фиксированные переменные из внешней области видимости (см. выше).

Локально объявленные переменные

Члены данных класса, объявленные внутри класса и this захваченные

Любая переменная, которая имеет статическую длительность хранения (например, глобальная переменная)

В следующем примере содержится лямбда-выражение, которое явно фиксирует переменную n по значению и неявно фиксирует переменную m по ссылке.

Поскольку переменная n фиксируется по значению, ее значение после вызова лямбда-выражения остается равным 0 . mutable Спецификацию можно n изменить в лямбда-выражении.

Несмотря на то что лямбда-выражение может фиксировать только переменные с автоматической длительностью хранения, в теле лямбда-выражения можно использовать переменные, которые имеют статическую длительность хранения. В следующем примере функция generate и лямбда-выражение используются для присвоения значения каждому элементу объекта vector . Лямбда-выражение изменяет статическую переменную для получения значения следующего элемента.

Дополнительные сведения см. в разделе Generate.

В следующем примере кода используется функция из предыдущего примера и добавляется пример лямбда-выражения, использующего алгоритм стандартной библиотеки C++ generate_n . Это лямбда-выражение назначает элемент объекта vector сумме предыдущих двух элементов. mutable Ключевое слово используется, чтобы тело лямбда-выражения может изменить свои копии внешних переменных x и y , которое захватывает лямбда-выражение по значению. Поскольку лямбда-выражение захватывает исходные переменные x и y по значению, их значения остаются равными 1 после выполнения лямбда-выражения.

Дополнительные сведения см. в разделе generate_n.

constexpr лямбда-выражения

Visual Studio 2017 версии 15,3 и более поздних версий (доступно в /std:c++17 ): лямбда-выражение может быть объявлено как constexpr или использоваться в константном выражении, когда инициализация каждого члена данных, который он захватывает или вводит, разрешена в константном выражении.

Лямбда-выражение неявно, constexpr если его результат удовлетворяет требованиям constexpr функции:

Если лямбда-выражение неявно или неявное constexpr , то преобразование в указатель функции создает constexpr функцию:

Специально для систем Майкрософт

Лямбда-выражения не поддерживаются в следующих управляемых сущностях среды CLR: ref class , ref struct , value class или value struct .

Если используется модификатор, зависящий от Майкрософт, такой как __declspec , его можно вставить в лямбда-выражение сразу после, например parameter-declaration-clause :

Чтобы определить, поддерживается ли модификатор лямбда-выражениями, см. статью о нем в разделе ” модификаторы Microsoft ” документации.

В дополнение к стандартным функциям лямбда-выражения C++ 11 Visual Studio поддерживает лямбда-выражения без отслеживания состояния, которые можно преобразовать в указатели функций, использующие произвольные соглашения о вызовах.

Прежде чем поговорить об устройстве, работе и диагностике лямбда- зонда, обратимся к некоторым особенностям работы топливной системы. Нам поможет в этом эксперт журнала, Федор Александрович Рязанов, диагност с большим стажем работы, руководитель курсов обучения диагностов в компании «ИнжКар».

Современный автомобилист хочет владеть мощным, но в тоже время экономичным автомобилем. У экологов другое требование – минимальное содержание вредных веществ в выхлопе машины. И в данных вопросах интересы автомобилистов и экологов в итоге совпадают. И вот почему.

Известно, что когда двигатель не сжигает все топливо, расход горючего возрастает, растут затраты и на эксплуатацию автомобиля. Мощность двигателя (или ДВС) в условиях неполного сгорания топлива неизбежно падает, а крутящий момент снижается. Одновременно с этим увеличивается уровень вредных веществ в выхлопе автомобиля.

В этой связи одной из основных задач современного автомобилестроения является максимально полное сжигание топливной смеси в двигателе.

На сжигание смеси прямым образом влияет ее состав. Идеальной ситуацией является стехиометрический состав топлива. Говоря более простым языком, должна быть соблюдена пропорция – на 14,7 кг воздуха должен приходиться 1 кг топлива. Именно такое соотношение позволяет оптимально использовать и то, и другое. Владелец автомобиля получает больший крутящий момент и, как следствие, — адекватное ускорение автомобиля, равномерную работу двигателя во всех режимах работы. Также падает расход топлива, и автомобиль перестает загрязнять окружающую среду.

Отклонения от правильного состава топливной смеси – богатая и бедная смесь. Богатая топливная смесь образуется, когда в цилиндрах мало кислорода, но много топлива, которое, конечно же, из-за недостатка кислорода, полностью сгореть не сможет. Следовательно, автомобиль, работающий на богатой смеси, будет больше расходовать топливо, а избыток несгоревшего топлива, в этом случае, охладит камеру сгорания, мощность двигателя при этом будет падать, несгоревшое топливо попадет в атмосферу, загрязняя ее.

Другая ситуация: двигатель получает обедненную топливную смесь. В этом случае топливо в цилиндрах будет сгорать не полностью из-за недостатка топлива. Об экономичности, ради которой и разрабатывались такие двигатели, в этом случае также придется забыть. Ведь бедная смесь плохо горит, и это автоматически приводит к падению крутящего момента. Водителю приходится больше нажимать на газ, что в свою очередь, ведет к перерасходу топлива.

Таким образом, понятно, что со всех аспектов только стехиометрия топливной смеси (пропорция 14,7/1) является самым оптимальным режимом работы двигателя. И, конечно же, автомобиль, который только-только сошел с конвейера, обычно, укладывается во все рамки этого критерия. Но и «заводская» настройка может отличаться от идеала. Более того, в процессе эксплуатации автомобиля неизбежно наступает износ некоторых компонентов, датчики, отвечающие за настройку топливной системы, могут терять точность настроек. В итоге состав топливной смеси все больше уходит от идеальных показателей.

В этом случае как раз и необходим лямбда- зонд, он фиксирует количество кислорода в выхлопе автомобиля. И если в выхлопе окажется большое количество кислорода, это «сигнализирует» о бедной топливной смеси и, наоборот, если в выхлопе нет кислорода, это указывает на то, что смесь стала богатой. А мы уже выяснили, что и в том, и в другом случае уменьшается мощность двигателя, растет расход топлива, снижается экологичность выхлопа. Задача лямбда-зонда как раз и заключается в том, чтобы скорректировать эти отклонения.

Возьмем в качестве примера такую ситуацию: в топливной системе засорились форсунки, их производительность снизилась, смесь стала обедненной. Лямба-зонд фиксирует этот факт, а блок управления топливной системой реагирует на эту информацию и «доливает» немного топлива в цилиндры. Так происходит корректировка возникающих отклонений с учетом показаний этого датчика.

Таким образом, основное назначение лямбда- зонда заключается в том, чтобы компенсировать неизбежно возникающие в процессе эксплуатации автомобиля отклонения в составе топливной смеси.

Однако нужно понимать, что лямбда-зонд как таковой не является панацеей от всех бед, он лишь позволяет вернуть состав топливной смеси в состояние стехиометрии. Но это не устранение дефектов, а только их компенсация.

Вернемся к нашим форсункам. При загрязненных форсунках нарушается эффективность распыления бензина, топливо распыляется крупными каплями, испаряются они с трудом. И система топливоподачи рассчитывает тот объем топлива, который необходим для достижения состояния стехиометрии, для этого фиксируются показания датчика расхода воздуха. Однако если бензин в системе выпрыскивается крупными каплями, его пары полностью не смешиваются с воздухом, часть паров сгорает, а часть капель бензина попросту вылетает в выхлопную трубу. Лямбда-зонд трактует такую ситуацию как бедную смесь, а датчик топливной системы, который «не видит» отдельные капли бензина, добавляет топлива, чтобы привести смесь в состояние стехиометрии. Но в этом случае, резко повышается расход топлива.

Поэтому для работы лямбда-зонда важен не фактор того, как система справляется с выводом смеси на стехиометрию, а фактор того, какой «ценой» ей удается это сделать.

Рассмотрим осциллограмму работы лямбда- зонда. Датчик сам по себе не может отличить состояние стехиометрии от состояния богатой топливной смеси, так как и в том, и в другом случае кислорода в выхлопе нет. При отсутствии кислорода в топливе блок управления (ЭБУ – электронный блок управления) немного уменьшает количество подаваемого в цилиндр топлива. Как следствие, в выхлопе появляется кислород.

И в этом случае показания лямбда-зонда находятся ниже отметки 0,4 В, что для датчика является признаком того, что топливная смесь обеднела (LEARN). При низких показателях лямбда-зонда (ниже 0,4 В), блок управления увеличивает подачу топлива на несколько процентов, смесь становится богатой и показания датчика достигают уровня выше 0,6В. ЭБУ воспринимает это как признак того, что в топливной системе находится богатая смесь (RICH). Подача топлива уменьшается, показания лябда-зонда падают, цикл повторяется — состав смеси начинает колебаться. В такт изменению состава смеси меняются показания лямбда-зонда. Такие колебания ЭБУ понимает как нормальное явление, указывающее на то, что состав топливной смеси находится в зоне стехиометрии.

Вспомним также, что в катализаторе автомобиля обязательно есть цирконий, этот металл способен накапливать кислород. И в фазе бедной смеси кислород запасается в катализаторе, а в фазе богатой смеси он расходуется. В результате на выходе топливной смеси катализатор дожигает все ее остатки.

На холостом ходу такие колебания возникают с частотой одно колебание примерно в одну секунду. Время такого переключения – еще один важный показатель для лямба-зонда. В нашем случае (см. осциллограмму, Рис. 1) время переключения составило 88 мс, при этом нормой является – 120 мс.

Если переключение длится долго, как в случае нашей осциллограммы (см. осциллограмму, Рис. 2) – 350 мс, да к тому же такая ситуация повторяется многократно, блок управления выдаст ошибку: «замедленная реакция лямбда-зонда».

Величины, при которых появляется эта ошибка, определяются, главным образом, настройками программного обеспечения блока управления.

Таким образом, для диагностики по лямбда-зонду необходимо изучить фазы переключения датчика. И если на осциллограмме появится хотя бы одно переключение с низкого показания на высокое (максимальное – 1В, минимальное – 0В), это значит, что лямбда-зонд работает исправно. Исправный датчик делает примерно одно переключение в секунду. Напомним, что в алгоритме работы блока управления о бедной смеси «сигналят» показания лямбда-зонда ниже 0,4В, а о богатой – выше 0,6 В. Поэтому оценить состояние топливной системы автомобиля можно и по работе датчика. В нашем случае (см. осциллограмму, Рис. 3) блоку управления удалось скомпенсировать все дефекты и вывести стехиометрию.

Вернемся к примеру с загрязненными форсунками. При обедненной смеси показания лямбда-зонда падают ниже 0,4В. Блок управления добавляет топлива до того момента, когда смесь станет богатой. Отметим, что в этом случае блок управления «самостоятельно» отклонился от установленных заводом-изготовителем в его карте параметров. Величину отклонения он записывает в своей памяти как топливную коррекцию (fuel trime). Предельно допустимые показатели топливной коррекции для большинства современных автомобилей составляют ±20-25%. Коррекция в «плюс» означает, что блоку пришлось добавлять топлива, коррекция в «минус» — наоборот, убавлять.

То есть важно помнить, что показатель топливной коррекции и работа лямбда-зонда – это комплексный параметр, он указывает на наличие дефекта, но не указывает конкретную причину, которую придется найти и устранить на автосервисе.

И немного об особенностях строения лямбда-зонда. Такой датчик имеет циркониевую колбочку, которая одной стороной помещена в выхлопные газы. Цирконий уникальный материал, так как сквозь него может проходить кислород. Ион кислорода, «прилипая» к атомам циркония, движется по ним, при этом на циркониевом колпачке возникает напряжение. И если все идет в штатном порядке, то диффузия ионов кислорода осуществляется равномерно, и напряжение на обкладках колбочки составляет 1В. Если в выхлопе появляется кислород, диффузия невозможна, и напряжение в этом случае равно 0В. Вместо циркония в лямбда-зондах может использоваться окись титана. Отличие циркониевого лямбда-зонда от титанового заключается в том, что первый вырабатывает напряжение, а другой – меняет свое сопротивление (в переделах от 0 до 5В), и ему нужна схема, которая переводит меняющееся сопротивление в напряжение.

Слой платины на колбочке поверх циркония позволяет снять с него напряжение, играет роль катализатора, дожигает бензин и несгоревший кислород. Все ухудшается при использовании некачественного топлива, а также топливных присадок, которые в прямом смысле закупоривают слой платины и циркония, и зонд выходит из строя. Однако в этом случае, если у зонда нет физических повреждений, обычная промывка вернет его в рабочее состояние. «Современный бич» – это добавки антидетонационных присадок в топливо. До недавнего времени в качестве присадки использовался ферроцент — опасное вещество, которое мы окрестили «красная смерть» за ее красный оттенок, а также за способность быстро выводить из строя свечи, лямбда-зонды и катализатор», — отмечает Федор Александрович. Зонд может «замерзнуть» в высоком или в низком положении, то есть или в фазе богатой, или в фазе бедной смеси. И в этом случае датчик достигнет пределов топливной коррекции и прекратит попытки выравнивать состав смеси до стехиометрии.

Диагностику состояния системы топливоподачи начинаем с подключения сканера к автомобилю. Отсутствие кода «Превышение пределов топливной коррекции» еще не говорит об отсутствии дефектов в системе топливоподачи. Необходимо в потоке данных (Data Stream) убедиться в наличии колебаний лямбда-зонда (стехиометрия достигнута), а также по величине топливной коррекции оценить, какой ценой она достигнута.

Подводя итог, еще раз отметим, что при проверке лямбда-зонда необходимо обращать внимание на колебания датчика, если они есть, датчик исправен; если же система лямбда регулирования не совершает колебаний, это может указывать или на неисправность лямбда-зонда или на бедную или богатую топливную смесь. То есть сначала надо проверить сами датчики. Для этого нужно принудительно обогатить или обеднить смесь, чтобы получить колебания лямбды и убедиться в том, что он исправен.

Рассмотренные выше лямбда-зонды носят название «скачковые». Т.е. они указывают на то, есть кислород в выхлопе или нет. Но все более ужесточающиеся требования к экологии заставили производителей разработать датчики, которые способны не только работать по принципу «Да-Нет», но и определять процент кисло- рода в выхлопе. Такие датчики получили название «широкополосные датчики кислорода».

Принципы их работы и особенности диагностики автомобиля по показаниям широкополосных лямбда-зондов будут рассмотрены в следующих публикациях.

Написать комментарий

Ваш комментарий: Внимание: HTML не поддерживается! Используйте обычный текст.